Sistema de ecuaciones

Publicado por Ecuación en 11:52 |

En las matemáticas, un sistema de ecuaciones es un conjunto de dos o más ecuaciones con variasincógnitas. Una solución para el sistema debe proporcionar un valor para cada incógnita, de manera que en ninguna de las ecuaciones del sistema se llegue a una contradicción. En otras palabras el valor que reemplazamos en las incógnitas debe hacer cumplir la igualdad del sistema.

Las incógnitas se suelen representar utilizando las últimas letras del alfabeto latino, o si son demasiadas, con subíndices.

Sistema general

La forma genérica de un sistema de m\, ecuaciones y n\, incógnitas es la siguiente:

(1)

\left\{\begin{matrix}F_1(x_1,...,x_n)=0 \\ \vdots \\ F_m(x_1,...,x_n)=0\end{matrix}\right.

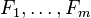donde F_1, \ldots, F_m son funciones de las incógnitas. La solución, perteneciente al espacio euclídeo \R^n , será tal que el resultado de evaluar cualquier expresión F_i\, con los valores de dicha solución, verifique la ecuación.

Representación gráfica

Los sistemas de 2 o 3 incógnitas admiten representaciones gráficas cuando las funciones F_i\, en (1) son continuas a tramos. En cada ecuación se representa como una curva o una superficie curva. La existencia de soluciones en ese caso puede deducirse a partir de la existencia de intersecciones comunes a dichas curvas o superficies curvas.

Clasificación de los sistemas

Un sistema de ecuaciones sobre \R^n puede clasificarse de acuerdo con el número de soluciones en:

  • Sistema incompatible cuando no admite ninguna solución.
  • Sistema compatible cuando admite alguna solución que a su vez pueden dividirse en:
    • Sistemas compatibles indeterminados cuando existe un número infinito de soluciones que forman una variedad continua.
    • Sistemas compatibles determinados cuando admiten un conjunto finito de soluciones, o un conjunto infinito de soluciones aisladas con a lo sumo un número finito de puntos de acumulación.

Sistema lineal


Un sistema como el anterior en que las anteriores ecuaciones son funciones afines. A diferencia del caso general, la solución de los sistemas de ecuaciones lineales son fáciles de encontrar cuando los coeficientes de las ecuaciones son números reales o complejos. También existen medios generales cuando los coeficientes pertenecen a un anillo, aunque la búsqueda de las soluciones en ese caso puede ser un poco más complicada.

Una característica importante de los sistemas lineales de ecuaciones es que admiten la llamada forma matricial. Esa forma permite representar el sistema usando tres matrices, de la siguiente forma:

(2)

\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1Y} \\ a_{21} & a_{22} & \cdots & a_{2Y} \\ \vdots & \vdots & \ddots & \vdots \\ a_{X1} & a_{X2} & \cdots & a_{XY} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_Y \end{pmatrix} = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_X \end{pmatrix}

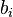La primera es la matriz de coeficientes, donde el término a_{ij}\, representa al coeficiente que acompaña a la j-ésima incógnita de la ecuación i-ésima. La segunda es la matriz de incógnitas, donde cada término se corresponde con una de las Y\, incógnitas que queremos averiguar. Y la tercera matriz es la de términos independientes, donde el cada b_i\, representa al término independiente de la ecuación i-ésima.

Esta representación matricial facilita el uso de algunos métodos de resolución, como el método de Gauss, en el que, partiendo de la matriz aumentada (matriz de coeficientes a la que se le ha acoplado la matriz de términos independientes), y aplicando transformaciones lineales sobre las ecuaciones, pretendemos llegar a una matriz de este tipo:

\begin{pmatrix} 1 & 0 & \cdots & 0 & b_1 \\ 0 & 1 & \cdots & 0 & b_2 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & b_X \end{pmatrix}

Una vez la matriz se ha triangulado, el valor de cada término 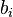b_i\, se corresponderá con el de la incógnita 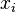x_i\,. Si nos encontramos alguna fila del tipo \begin{pmatrix}0 & 0 & 0 & b_X \\\end{pmatrix}, con b_X\ne0\,, el sistema no tendrá solución.

kashdjsbhsdhshusdhjshs

Existencia de soluciones

El teorema de la función inversa proporciona condiciones suficientes de existencia de solución, de un sistema como (1) con m = n\,. Si sucede que la función vectorial:

\mathbf{F}:\R^n \longrightarrow \R^n, \qquad (x_1,\dots,x_n) \mapsto (F_1(x_1,\dots,x_n),\dots,F_n(x_1,\dots,x_n))

Es diferenciable con continuidad, es decir, es de clase C^1(\R^n) y su jacobiano no se anula en ningún punto entonces existe una única solución del sistema (1). Ya que en ese caso existirá una función inversa, y podremos escribir la solución buscada simplemente como:

(x_1,\dots,x_n)=\mathbf{F}^{-1}(\mathbf{0})

Sin embargo, la condición de diferenciabilidad anterior aún siendo condición suficiente, no es una condición necesaria, por lo que existen sistemas de ecuaciones en que las funciones F_i\, no son diferenciables y sin embargo, existen soluciones. Más aún, en casos en que existe más de una solución si la función es diferenciable entonces el jacobiano se anula en algún punto, pero eso no impide que existan varias soluciones.

En casos de un menor número de ecuaciones que de incógnitas, cuando m < n\,, entonces el sistema es compatible indeterminado o carece de soluciones. En esos casos, el teorema de la función implícita proporciona condiciones suficientes, aunque no necesarias, para la existencia de soluciones de un modo similar a como el teorema de la función inversa las proporciona en el caso m = n\,.

Métodos de resolución

Si bien para los sistemas de ecuaciones lineales existen multitud de técnicas del álgebra lineal, para los sistemas de ecuaciones no-lineales el problema es técnicamente bastante más difícil.
| martes, 8 de septiembre de 2009

0 comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)